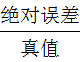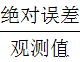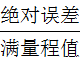誤差分析
1. 測量誤差的分類
表9-4列出了測量誤差的分類及其定義
表9-4 測量誤差的分類及其定義
|
分類方法 |
定義 |
說明 |
|
按誤差表達形式分類 |
(1) 絕對誤差=觀測值-真值
≈觀測值-觀測值的算術平均值(偏差)
(2) 相對誤差=
≈
(3) 引用誤差(滿度誤差)
= |
實際分析中,一般真值是未知的,常以觀測值的平均值代替真值,以偏差代替絕對誤差
傳感器、多檔和連續刻度的儀表的精度等級,通常按引用誤差劃分,為減少示值誤差,應盡可能在其滿量程值的1/3以上量程內進行測量 |
|
按誤差性質及產生原因分類 |
(1) 系統誤差:是指服從某一確定規律的誤差,常由儀器、裝置、人身、環境、理論誤差等引起
(2) 隨機誤差:是由于某些難以控制的偶然性因素引起的誤差,就總體而言它服從統計規律
(3) 過失誤差:主要是由于測試人員粗枝大葉,過度疲勞或操作不當引起的,一般可避免
|
因通過對測量數據的統計處理不一定能發現和消除系統誤差,故若存在著某項系統誤差而不知道。是極為不利的。系統誤差的產生原因往往可知或能掌握,應首先盡可能設法預見到各種系統誤差的具體來源并設法消除,其次設法估計出未能消除的系統誤差值。
在測量次數極多而測量的分辨率又極高的情況下,絕大多數隨機誤差是服從正態分布的。
含有過失誤差的數據稱異常值,它將會歪曲試驗結果,必須將其剔除,常用物理剔除法和統計判別法剔除。 |
2. 隨機誤差的正態分布
對某被測量在同一條件下多次重復測量,在得到的一系列僅含有隨機誤差的測定值中,從整體來看,發現隨機誤差具有以下特征:
a. 絕對值相等的正誤差與負誤差出現的機會相等。
b. 絕對值小的誤差比絕對值大的誤差出現的機會多。
c. 在一定的測量條件下,隨機誤差的絕對值不會超過一定界限。
d. 隨著測量次數的無限增加,隨機誤差的算術平均值趨向于零。